Blog de SRR

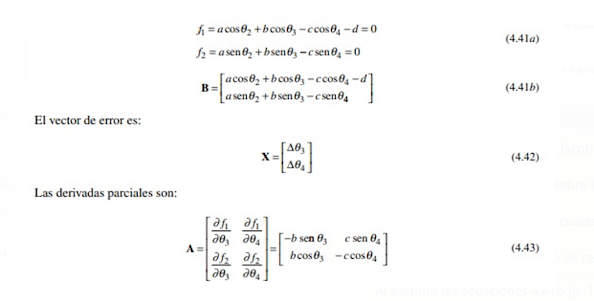
La ecuación de lazo vectorial del mecanismo de cuatro barras, separada en sus partes real e imaginaria (ecuaciones 4.6a y 4.6b, p. 166), proporciona el conjunto de ecuaciones que definen los dos ángulos de eslabón desconocidos, q3 y q4. Se usan las longitudes de eslabón a, b, c, d y el ángulo de entrada q2. Esta matriz se conoce como el Jacobiano del sistema; además de su utilidad en este método de solución, también indica algo sobre la resolución del sistema. El sistema de ecuaciones de posición, velocidad y aceleración (en las cuales aparece el Jacobiano) sólo puede resolverse si el valor del determinante del Jacobiano no es cero. Al sustituir las ecuaciones 4.41b (p. 183), 4.42 y 4.43 (p. 183) en la ecuación 4.40 (p. 183) se obtiene: Para resolver esta ecuación matricial se tendrán que suponer valores para q3 y q4 y las dos ecuaciones se resolverán de manera simultánea para Δq3 y Δq4. Para un sistema más grande de ecuaciones, se tendrá que utilizar un algoritmo de reducción de mat

Un centro instantáneo de velocidad se define como un punto común a dos cuerpos en movimiento plano que tiene la misma velocidad instantánea en cada cuerpo. Los centros instantáneos en ocasiones también se denominan centros o polos. Puesto que se requieren dos cuerpos o eslabones para crear un centro instantáneo (IC, por sus siglas en inglés), se puede predecir con facilidad la cantidad de centros instantáneos que se puede esperar en cualquier conjunto de eslabones. La fórmula para la combinación de n cosas tomadas de r a la vez es: Por la ecuación 6.8b, se puede ver que un mecanismo de cuatro barras tiene 6 centros instantáneos, uno de seis tiene 15 y uno de ocho tiene 28. La figura 6-5 (p. 252) muestra un mecanismo de cuatro barras en una posición arbitraria. También muestra una gráfica lineal que es útil para rastrear los centros instantáneos encontrados. Esta gráfica particular puede crearse al trazar un círculo en el cual se marcan tantos puntos como eslabones hay en el ensamble.

Los ángulos de los eslabones de entrada que corresponden a las posiciones de agarrotamiento (configuraciones estacionarias) del mecanismo de triple balancín de no Grashof se calculan con el siguiente método mediante trigonometría. La figura 4-17 muestra un mecanismo de cuatro barras de no Grashof en una posición general. Se trazó una línea de construcción h entre los puntos A y O4. Ésta divide el lazo cuadrilateral en dos triángulos, O2AO4 y ABO4. La ecuación 4.31 utiliza la ley de cosenos para expresar el ángulo de transmisión m en función de las longitudes de los eslabones y los ángulos del eslabón de entrada q2. por lo tanto: Para encontrar los valores del ángulo de entrada q2 máximo y mínimo, se puede diferenciar la ecuación 4.31, al derivar q2 con respecto a m e igualar a cero. Las longitudes de los eslabones a, b, c, d nunca son cero, de modo que esta expresión sólo puede ser cero cuando sen m es cero. Esto será cierto cuando el ángulo m en la fi gura 4-17 es cero o 180°. Est

Los métodos de solución para análisis de posición mostrados hasta ahora en este capítulo son de “forma cerrada” lo que significa que proporcionan la solución con un método directo no iterativo. * En algunas situaciones, en particular con mecanismos de lazos múltiples, una solución de forma cerrada puede no ser factible. En tal caso, se requiere un método iterativo y el método de Newton-Raphson (en ocasiones llamado sólo método de Newton) es uno que puede resolver conjuntos de ecuaciones simultáneas no lineales. Cualquier método de solución iterativo requiere uno o más valores supuestos para iniciar el cálculo. Luego los utiliza para obtener una solución nueva que puede aproximarse a la correcta. Este proceso se repite hasta que converge en una solución suficientemente próxima a la correcta para propósitos prácticos. Sin embargo, no existe garantía de que un método iterativo convergirá. Puede divergir y dar soluciones sucesivas que se alejan de la correcta, en especial si la suposición